웹에서 수집한 데이터에서 전화번호를 키 값으로 음식점명을 추출했을 때 아래와 같은 결과가 나왔다.
1. 02-123-4567 메이필드호텔 봉래정
2. 02-123-4567 봉래정(메이필드호텔)
3. 02-123-4567 카페 라리
사람 이 봤을 때 1번 문서 “메이필드호텔 봉래정” 과 2번 문서 “봉래정(메이필드호텔)”은 분명 다른 스트링이지만 같은 음식점을 지칭한다. 하지만 3번 문서 “카페 라리” 는 앞의 두개와는 전혀 다른 정보이다. 어떤 부류가 해당 전화 번호의 음식점인지는 직접 전화를 걸어보면 알겠지만, 그 사실 여부는 차치하고라도, 사람은 이 데이터 만으로 한 전화 번호에 두 개의 식당이 존재한다는 것을 판단을 할 수 있다.
이러한 것을 기계적으로 어떻게 판단 할까? 간단히 생각하면 각 스트링을 띄어쓰기 단위로 키워드를 추출하여 해당 키워드가 포함되어 있는 스트링을 추출해 내는 작업을 모든 키워드에 대하여 작업을 하면 될 것이다. 하지만, 이런 경우는 어떻게 하나..
1. 02-234-5678 카페 가네
2. 02-234-5678 가네
3. 02-234-5678 신가네김밥
키워드 “가네”가 3번 문서 “신가네 김밥”에도 포함되어 있으므로 같은 음식점으로 오판을 하고 만다. 이 외에도 여러 예외 사항이 있을 것이다. 인공지능을 공부한 사람답게 좀 더 인공지능적으로 해결을 해 보자. 이 경우는 여러 데이터들을 어떻게 분류(classification) 또는 군집(clustering) 하는가 중, clustering에 해당 한다고 볼 수 있다. 신경망, svm 등의 학습 기반 방법을 쓸 수도 있겠지만, 대량의 학습 데이터를 만드는 것도 일이 거니와, 데이터의 형태가 너무도 다양하다. 여기서는 그렇게 복잡한 방법 말고 단순히 IR에서 문서의 유사도를 계산하는데 사용되는 코사인 유사도 계산등의 방법으로도 효과가 상당할 것 같다. 하지만 이것을 현재 문제에 적용하기에는 좀 부족하다. key 02-123-4567을 가지고 좀 더 단순화 해 보자.
각 문서의 스트링에서 단어를 추출하면 “메이필드호텔”, “봉래정”, “카페”, “라리” 총 네 개의 단어를 뽑을 수가 있다. 형태소 분석기를 사용하게 되면 “메이필드”, “호텔” 로 더 쪼개서 총 다섯개의 단어를 뽑을 수도 있겠지만, 여기서는 문제 해결을 위한 과정을 단순화 하기 위해 “메이필드호텔”, “봉래정”, “카페”, “라리” 네개의 단어를 사용하자. 이렇게 뽑은 키워드를 비트로 표현하면 각 문서는 아래와 같은 벡터로 표현 될 수 있다.
1.(1, 1, 0, 0)
2.(1, 1, 0, 0)
3.(0, 0, 1, 1)
모든 벡터가 0, 1 로 표현되는 이진 벡터의 경우는 해밍 거리(hamming distance) 를 적용할 수 있다. 해밍 거리는 서로 다른 비트의 개수를 센다. 예를 들어 (1, 0, 1, 0), (0, 0, 1, 1) 일 때 거리는 2 이다. 가질 수 있는 거리의 최대값을 distancemax 라 할 때, 문서 a, b 에 대한 유사도 similaritya,b 는 아래와 같이 구할 수 있다.
이를 이용해서 유사도를 계산해 보면 아래와 같다.
s1,3=4-4=0
s2,3=4-4=0
음… 이래서는 곤란하다. 관계 없는 (1, 3), (2, 3) 이 유사도가 2로 높게 나온다. 단순히 벡터간의 거리만을 판단하기 때문에 이런 결과가 나온다.(예를 잘못 들었다) 실제 문서상에서 해당 단어가 존재하는지 여부가 중요한데 이 부분이 고려 되지 않았다.
다시 코사인 유사도를 생각을 해 보자. 문서 a 가 wa1, wa2, wa3… 의 키워드를 가지고 있고, 문서 b 가 wb1, wb2, wb3의 키워드를 가지고 있을 때, a 는 벡터 (wa1, wa2, wa3…), b 는 벡터 (wb1, wb2, wb3…) 로 나타낼 수 있다. 이 때, 문서 a b 간의 코사인 유사도는 아래와 같은 공식으로 계산 할 수 있다.
이를 풀어 쓰면 아래와 같다.

이를 위에서 변환한 이진 벡터로 적용을 해 보면 a.b 의 내적은 결국 둘다 1인 비트의 갯수가 되고, 각 벡터의 길이는 1인 비트의 갯수와 대략 비슷하게 된다. 이것을 a, b 둘다 있는 경우, a엔 있지만 b에 없는 경우, 반대로 b엔 있지만 a에는 없는 경우 등을 고려 한다. 그러면 유사도 계산식은 아래와 같이 간략화 할 수 있다.

여기서 n11은 문서 a, b 모두 1인 비트 수, n10은 문서 a 만 1인 비트 수, n01은 문서 b 만 1인 비트 수 이다.
이 식을 가지고 key 02-123-4567 의 문서들의 유사도를 계산 해 보자.

즉, 문서 1,2 는 유사도가 1이고 1,3 2,3 은 유사도가 0이다. 유사도 계산값이 0보다 큰 것만 골라 내면 될 것이다. 그러면 1, 2 두개의 문서가 묶인 부류 하나와 3 혼자 있는 부류 하나 해서 두개의 부류를 얻게 된다.
좀 더 많은 문서와 단어를 가지고 더 살펴 보자.
1.A B (1, 1, 0, 0, 0, 0)
2.A D (1, 0, 0, 1, 0, 0)
3.B (0, 1, 0, 0, 0, 0)
4.E F (0, 0, 0, 0, 1, 1)
5.E (0, 0, 0, 0, 1, 0)
6.D (0, 0, 0, 1, 0, 0)

유사도가 0보다 큰 것들만 뽑으면 (1,2), (1,3), (2,6), (4,5) 이다. 이를 문서번호로 이진트리로 그려보자.
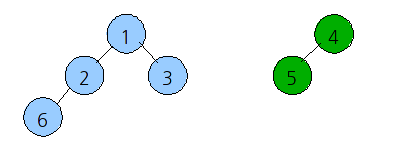
4(E F), 5(E)
이렇게 두개로 구분을 할 수가 있게 된다.
이러한 작업이 가능하기 위한 선행 작업으로 먼저 각 단어를 잘 뽑아 낼 수가 있어야 하고, 이를 위해서는 형태소 분석이나 단어 사전을 잘 구축을 해야 한다. 현재 상황에서는 음식점명들이 대부분 명사이기 때문에 전체 음식명들을 가지고 띄어쓰기 단위나, (, ), [, ], – 등을 구분자로 사용하여 키워드만 추출을 잘 해도 단어 사전을 기계적으로 쉽게 구축 할 수가 있다.
이 아이디어를 바탕으로 이제 실제 구현만 하면 되겠다. 검색의 품질을 높이는데 있어서 색인기, 쿼리 분석기 등의 엔진단도 중요하지만, 색인 데이터를 얼마나 잘 정제해서 엔진에 넣느냐는 데이터 마이닝도 무척 중요하다고 생각한다. 구현을 마치고 서비스에 적용을 했을 때, 맛집 검색의 그룹핑 정확도가 좀 더 높아질것이라 기대한다.
reference :
1. 코사인 유사도 cosine similarity http://en.wikipedia.org/wiki/Cosine_similarity
2. 내적 http://ko.wikipedia.org/wiki/%EB%82%B4%EC%A0%81
2-1. inner product http://en.wikipedia.org/wiki/Inner_product
3. 해밍 거리 http://ko.wikipedia.org/wiki/%ED%95%B4%EB%B0%8D_%EA%B1%B0%EB%A6%AC
3-1. hamming distance http://en.wikipedia.org/wiki/Hamming_distance
secret comment.
댓글이 달려 있어 다시 읽다 보니, 해밍거리 구하는 것을 예를 잘못 들었네요. 구현 하다보니 해밍거리 만으로는 애매해 지는 상황이 발생해서 설명하려고 했던 것인데, 그 부분만 생각하고 글을 작성하다 보니 실수를 했습니다. 덕분에 오류를 수정했네요. ^^
프로젝트 잘 마무리 되시길 바랍니다.
좋은글 잘 읽었습니다.
감사합니다.
cos() 식에서 이진 적용해서 similarity 으로 넘여가는 과정이 궁금합니다. similarity 가 Jaccard_coefficient 인것 같은데.. http://en.wikipedia.org/wiki/Jaccard_coefficient
수학적 지식이 부족해서요.. 어떻게 넘어가는 거죠? ㅠㅜ
많은 도움이 되었습니다. 감사합니다 :)
쟈카드 계수는 코사인 유사도에서 유도된 것이 아닙니다.
단순 매칭 계수(SMC)에서 유도된 것입니다.
SMC는 이진 속성으로만 표현되는 경우에 유사도를 측정하는 방식인데, 0의 값이 의미가 없는 특별한 경우에(본문의 예의 경우) , 즉 양쪽 모두 0을 갖는 f00 빈도수를 제거하고 계산하는 것이 쟈카드 계수입니다.
http://socurites.com/144